We need your help! 🔥
Please consider disabling your ad-blocker to support this website! 🔑
We are a free, community-supported website! 🥰
We only display small unobtrusive ads which help us stay online! 💯
Thank you in advance! ❤️
We are a free, community-supported website! 🥰
We only display small unobtrusive ads which help us stay online! 💯
Thank you in advance! ❤️
Parakeet
ADDON. Version 0.6.1. Released on 2019-Oct-13. Provides 119 components. Created by Esmaeil. Features 6 video tutorials.
Parakeet is a collection of components focusing in Algorithmic Pattern Generation; it offers a Unique and easy-to-use approach that Generates Geometrical and Natural Patterns/Networks. For now, Parakeet has 8 Categories: Tilings, Primitives, Pattern Generation, Curve, Mesh, Surface, M.C. Escher and utilities.
Tiling
| Pentagonal Tiling 07 (PTiling 07) Creates a Euclidean Iregular Pentagonal tiling | |
| Pentagonal Tiling 10 (PTiling 10) Creates a Euclidean Iregular Pentagonal tiling | |
| 2-Uniform Tiling E (2TilingE) Creates a Euclidean 2-Uniform tiling consisting of convex polygons with vertex configuration of ([4.3.12.3; 12.12.3]) | |
| 2-Uniform Tiling A (2TilingA) Creates a Euclidean 2-Uniform tiling consisting of convex polygons with vertex configuration of ([3.4.6.4 ; 3^2.4.3.4]) | |
| Pentagonal Tiling 15 (PTiling 15) Creates a Euclidean Iregular Pentagonal tiling | |
| Pentagonal Tiling 02_A (PTiling 02A) Creates a Euclidean Iregular Pentagonal tiling | |
| Snub square (Tiling B sr) Creates a Euclidean semi-regular tiling consisting of convex polygons with vertex configuration of (3.3.4.3.4), also known as Snub square Tiling | |
| Pentagonal Tiling 01_A (PTiling 01A) Creates a Euclidean Iregular Pentagonal tiling | |
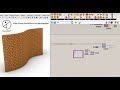
| Brick Type H (Brick H) Creates Bricks as closed polylines (Cell) on a Surface | |
| Trihexagonal (Tiling G sr) Creates a Euclidean semi-regular tiling consisting of convex polygons with vertex configuration of (3.6.6), also known as Trihexagonal tiling | |
| Pentagonal Tiling 13 (PTiling 13) Creates a Euclidean Iregular Pentagonal tiling | |
| Brick Type I (Brick I) Creates Bricks as closed polylines (Cell) on a Surface | |
| Truncated hexagonal (Tiling E sr) Creates a Euclidean semi-regular tiling consisting of convex polygons with vertex configuration of (3.12.12), also known as Truncated hexagonal tiling | |
| Snub Trihexagonal (Tiling A sr) Creates a Euclidean semi-regular tiling consisting of convex polygons with vertex configuration of (3.3.3.3.6), also known as Snub Trihexagonal tiling. | |
| 2-Uniform Tiling B (2TilingB) Creates a Euclidean 2-Uniform tiling consisting of convex polygons with vertex configuration of ([4.6.12 ; 3.4.6.4]) | |
| 2-Uniform Tiling F (2TilingF) Creates a Euclidean 2-Uniform tiling consisting of convex polygons with vertex configuration of ([3^6; 3^2.4.12]) | |
| Trilateral Tiling I (TriTiling I) Generates a Tiling (Grid) based on any irregular/regular Trilateral Curve (any Closed Polyline with 3 points and 3 edges) | |
| Trilateral Tiling II (TriTiling II) Generates a Tiling (Grid) based on any irregular/regular Trilateral Curve (any Closed Polyline with 3 points and 3 edges) | |
| Truncated square (Tiling D sr) Creates a Euclidean semi-regular tiling consisting of convex polygons with vertex configuration of (4.8.8), also known as Truncated square tiling | |
| Pentagonal Tiling 06 (PTiling 06) Creates a Euclidean Iregular Pentagonal tiling | |
| Quadrilateral Tiling (QuadTiling) Generates a Tiling (Grid) based on any irregular/regular Quadrilateral Curve (any Closed Polyline with 4 points and 4 edges) | |
| Truncated trihexagonal (Tiling F sr) Creates a Euclidean semi-regular tiling consisting of convex polygons with vertex configuration of (4.6.12), also known as Truncated trihexagonal tiling | |
| 2-Uniform Tiling D (2TilingD) Creates a Euclidean 2-Uniform tiling consisting of convex polygons with vertex configuration of ([3.3.4.3.4; 4.4.3.3.3]) | |
| Brick Type G (Brick G) Creates Bricks as closed polylines (Cell) on a Surface | |
| Pentagonal Tiling 01_B (PTiling 01B) Creates a Euclidean Iregular Pentagonal tiling | |
| Brick Type J (Brick J) Creates Bricks as closed polylines (Cell) on a Surface | |
| Pentagonal Tiling 09 (PTiling 09) Creates a Euclidean Iregular Pentagonal tiling | |
| Pentagonal Tiling 02_B (PTiling 02B) Creates a Euclidean Iregular Pentagonal tiling | |
| Brick Type D (Brick D) Creates Bricks as closed polylines (Cell) on a Surface | |
| Rhombitrihexagonal (Tiling C sr) Creates a Euclidean semi-regular tiling consisting of convex polygons with vertex configuration of (3.4.6.4), also known as Rhombitrihexagonal tiling | |
| Brick Type C (Brick C) Creates Bricks as closed polylines (Cell) on a Surface | |
| Brick Type B (Brick B) Creates Bricks as closed polylines (Cell) on a Surface | |
| Elongated triangular (Tiling H sr) Creates a Euclidean semi-regular tiling consisting of convex polygons with vertex configuration of (3.3.3.4.4), also known as Elongated triangular tiling | |
| 2-Uniform Tiling C (2TilingC) Creates a Euclidean 2-Uniform tiling consisting of convex polygons with vertex configuration of ([3.3.3.4.4; 6.4.3.4]) | |
| Penrose Creates a Penrose Tiling(Penrose of Type 2) Consisting of Quadrilateral Polygons | |
| Brick Type E (Brick E) Creates Bricks as closed polylines (Cell) on a Surface | |
| Brick Type A (Brick A) Creates Bricks as closed polylines (Cell) on a Surface | |
| Brick Type F (Brick F) Creates Bricks as closed polylines (Cell) on a Surface |
Pattern Generation
| Pattern Genotype E (PatternGenE) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Tileable Pattern (p4) (Tilep4) A Method for Generating Tileable Patterns. | |
| Tileable Pattern (pmg) (Tilepmg) A Method for Generating Tileable Patterns. | |
| Pattern Genotype N (TA) (PatternGenN) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Shared under Creative Common License “Attribution-ShareAlike” (CC BY-SA)] | |
| 2D Aggregation Generates an aggregated system consist of an arbitrary base curve | |
| Cymatic Pattern (Cymatics) [Experimental Component] Creates Cymatic patterns (Also Known as Chladni Plates; https://monoskop.org/Ernst_Chladni) | |
| Pattern Statistics (PatternStat) Retrieves some statistics regarding a Pattern (Network of Lines/Curves) | |
| Gilbert Tesselation C (GilbertC) Generates a Pattern Based on a re-envision of Gilbert Tessellation. Shared under Attribution-NonCommercial license (CC BY-NC), Contact Support Email for Commercial use | |
| Pattern Genotype G (PatternGenG) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) | |
| Pattern Genotype K (PatternGenK) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Star Pattern II (StarPatternII) a Geometrical method for designing Islamic Patterns (Based on a method presented by Hankin Lee & Craig S | |
| Pattern Genotype I (PatternGenI) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) | |
| Pattern Genotype M (PT) (PatternGenM (PT)) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) | This Genotype returens Pentognal Tilings (Known as Pentagonal Tilings of Type 3) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Tileable Pattern (pmm) (Tilepmm) A Method for Generating Tileable Patterns. | |
| Pattern Genotype L (PT) (PatternGenL (PT)) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) | This Genotype returens Pentognal Tilings (Known as Pentagonal Tilings of Type 4 and 5) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Star Pattern I (StarPatternI) a Geometrical method for designing Islamic Patterns (Based on a method presented by Craig S | |
| Pattern Genotype J (PatternGenJ) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) | |
| Pattern Genotype C (PatternGenC) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Tileable Pattern (p4m) (Tilep4m) A Method for Generating Tileable Patterns. | |
| Pattern Genotype H (PatternGenH) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Venation Generates a Venetaion [Branching] Network of Curves among a List of Points | |
| Pattern Genotype B (PatternGenB) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Pattern Genotype F (PatternGenF) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Tileable Pattern (p4g) (Tilep4g) A Method for Generating Tileable Patterns. | |
| Flow Path (Flow) Generates a [Discrete] Fluid Flow Path on a Mesh | |
| Fractal Polyline (Fractal) Generates a Fractal Polyline | |
| Growth (GrowthA) Generates a Single-Polyline Pattern, resembling Natural Growth of Cells and Organs [also Known by name of ‘Differential Growth’] Connect a Grasshopper Timer to refresh the Component | |
| Maze Generates a Perfect Maze (Based on Backtracking Algorithm) Based on a Given Mesh | |
| Pattern Genotype A (PatternGenA) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Gilbert Tesselation B (GilbertB) Generates a Pattern Based on a re-envision of Gilbert Tessellation. Shared under Attribution-NonCommercial license (CC BY-NC), Contact Support Email for Commercial use | |
| Pattern Genotype D (PatternGenD) a Method of Generating Patterns on Custom Cells (Hint: Works Best with Cells from Parakeet’s “Tiling” Category) [Based on Esmaeil Mottaghi’s Dissertation [See https://www | |
| Tileable Pattern (pgg) (Tilepgg) A Method for Generating Tileable Patterns. | |
| Gilbert Tesselation A (GilbertA) Generates a Pattern Based on a re-envision of Gilbert Tessellation. Shared under Attribution-NonCommercial license (CC BY-NC), Contact Support Email for Commercial use | |
| Knit Generates a Knitted Pattern on a Surface | |
| Kelidoscope Generates a Pattern based on ‘kaleidoscope’ Mechanism. Shared under Attribution-NonCommercial license (CC BY-NC), Contact Support Email for Commercial use | |
| 3D Aggregation Generates an aggregated system consist of an arbitrary base mesh |
Surface
| RemoveDuplicateSurface (RemoveDupSrf) Removes identical Surfaces from a List | |
| Map To Surface (MapToSrf) map a Curve onto a Surface | |
| Panelized Sum Surface (PQSumSrf) Creates a Planar Quad panelization on a surface, generated by two profile curves(based on a method by Mr.Tang https://geometry.stanford.edu/person.php?id=tangcc) | |
| Extend Surface (ExtendSrf) Extends a surface by specified edge and distance | |
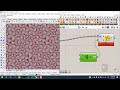
| Voronoi On Surface (VoronoiSrf) Generates a Voroni pattern on given Nurbs surface | |
| Offset Brep (BrepOffset) Offset a Brep with variable parameters | |
| CreateSolid Creates a Solid (Closed Brep) Enclosed by Intersecting Surfaces and PolySurfaces | |
| Reverse Surface (ReverseSrf) Reverses U and V direction (domain) of a surface | |
| Brep Topology Retrieves full topology of Brep | |
| Brep Remove Holes (BrepRemoveHoles) Removes Holes of a B-rep (Works with both Trimmed and Untrimmed Nurbs Surface(s)) | |
| BooleanSplit Splits a Brep with Other Brep(s) [Brep|Brep Split] |
Util
| Reflection Point (ReflectP) Returnes Reflection of a [List of] Points from a Plane | |
| Clean Number (CleanNumber) Converts scientific format (and other numercial formats) to plain numbers | |
| Mouse Retrieves cursor coordinates and status of mouse buttons | |
| FaceMe Plane (FaceMe) Generates a Plane facing the active camera (a 'Timer' Should be connected ro rerun the component) | |
| Golden Point (GoldenPt) Creates a Point [C] on a Given Line [AB] where AC/BC=φ (Golden Ratio ≈ 2.618) | |
| Interpolate Color Interpolates a Collection of Colors | |
| Zoom to (Zoom) Sets Camera to a certain Distance Targeting a Point | |
| Custom Round Rounds a Number by custom scope | |
| Scissors (Scissor) Simulates Deployable Circular Scissor Structure |
Curve
| Mirrored Subdivide Quad (QuadSubM) Subdivides Closed Polygon into Quad Cells and mirrors the pieces alternately (Usefull for Generating Geometrical Patterns) | |
| Network Topology Retrieves full topology of a network of Lines | |
| Polygon by Area (Polygon Area) Creates a Polygon based on specified area | |
| Random Seam Randomly adjusts the seam of given curves (and Polylines) | |
| Dual Garph (Dual) Generates the Dual graph for a List of Polygons | |
| Align Curves (AlignCrv) Aligns a List of Curves Based on a Guide Curve by Adjusting Both Curve Seam and Direction | |
| Divide Curve Variable (DivideVar) Divides a curve based on Curvature with variable parameters | |
| Loop Trancate (Trancate) Truncates a Pattern (2D or 3D Network of Lines/Curves) recursivly | |
| Map Curves (MapCrv2Crv) Maps a Collaction of Polylines and Curves from one Polyline to another Polyline. Source and Target Polylines must have same number of Vertices (or Segments). |
M.C.Escher Tilings
| Meta Escher Trilateral (MetaEscherTri) Generates a Heterogeneous Tiling (Deformation Parquet) of Custom Curves Based on a Trilateral (Triangular) Grid [Best Known from Drawings of M.C.Escher (1898-1972)] | |
| Escher Hexagonal B (EscherHexB) Generates a Tiling of Custom Curves Based on a Square Grid [Best Known from Drawings of M. C. Escher (1898-1972)] | |
| Meta Escher Hexagonal A (MetaEscherHexA) Generates a Heterogeneous Tiling (Deformation Parquet) of Custom Curves Based on a Hexagonal Grid [Best Known from Drawings of M.C.Escher (1898-1972)] | |
| Escher Quadriladeral A (EscherQuadA) Generates a Tiling of Custom Curves Based on a Square Grid [Best Known from Drawings of M. C. Escher (1898-1972)] | |
| Escher Hexagonal A (EscherHexA) Generates a Tiling of Custom Curves Based on a Square Grid [Best Known from Drawings of M. C. Escher (1898-1972)] | |
| Meta Escher Quadriladeral (MetaEscherQuad) Generates a Heterogeneous Tiling (Deformation Parquet) of Custom Curves Based on a Quadriladeral (Square) Grid [Best Known from Drawings of M.C.Escher (1898-1972)] | |
| Meta Escher Hexagonal B (MetaEscherHexB) Generates a Heterogeneous Tiling (Deformation Parquet) of Custom Curves Based on a Hexagonal Grid [Best Known from Drawings of M.C.Escher (1898-1972)] | |
| Escher Trilateral A (EscherTriA) Generates a Tiling of Custom Curves Based on a Square Grid [Best Known from Drawings of M. C. Escher (1898-1972)] |
Primitive
| Klein Surface Creates a Klien Nurbs surface | |
| Klein Bottle Creates a Klien bottle as a Nurbs surface | |
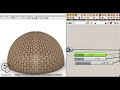
| Geodesic Dome Generates a Geodesic Dome based on a Icosahedron | |
| PlukerSurface (PlukerSrf) Creates a Plucker surface with variable parameters | |
| Mobius Surface (Mobius) Creates a Mobius surface with variable parameters |
Mesh
| MeshCap Caps all holes by covering Naked Edges | |
| Mesh Surface Variable (MeshSrfVar) Creates a Mesh based on curvature of base surface (Larger mesh faces in flat areas) | |
| Mesh Topology Retrieves full topology of Mesh |
Site design © Robin Rodricks.
Site co-created by Andrew Heumann.
Parakeet and associated data © 2025 Esmaeil.
Rhinoceros and Grasshopper are registered trademarks of Robert McNeel & Associates.
Hosted by GitHub