We need your help! 🔥
Please consider disabling your ad-blocker to support this website! 🔑
We are a free, community-supported website! 🥰
We only display small unobtrusive ads which help us stay online! 💯
Thank you in advance! ❤️
We are a free, community-supported website! 🥰
We only display small unobtrusive ads which help us stay online! 💯
Thank you in advance! ❤️
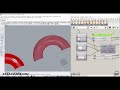
Surface Edit Points
Extract the edit points on a surface at knot averages, the points an interpolated surface interpolated through.
Inputs
| Name | ID | Description | Type |
|---|---|---|---|
| Surface | S | Surface to get the edit points of | Surface |
| Knots | K | If True, only the edit points at knots (span ends) are extracted (the points an interpolated surface interpolated through) If False, all edit points are extracted which equals the same amount as the surface control points | Boolean |
Outputs
| Name | ID | Description | Type |
|---|---|---|---|
| Points | P | Edit points on the surface | Point |
| Normals | N | Normal vectors at edit points | Vector |
| Count U | U | Number of edit points along the surface {u} direction | Integer |
| Count V | V | Number of edit points along the surface {v} direction | Integer |
| Parameters | uv | Parameter coordinates at edit points | Point |
Site design © Robin Rodricks.
Pufferfish and associated data © 2025 Michael Pryor.
Rhinoceros and Grasshopper are registered trademarks of Robert McNeel & Associates.
Hosted by GitHub