We need your help! 🔥
Please consider disabling your ad-blocker to support this website! 🔑
We are a free, community-supported website! 🥰
We only display small unobtrusive ads which help us stay online! 💯
Thank you in advance! ❤️
We are a free, community-supported website! 🥰
We only display small unobtrusive ads which help us stay online! 💯
Thank you in advance! ❤️
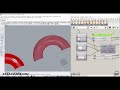
Tween Through Planes On Surface
Tween through a set of planes on a surface, if plane origins are not on the surface they will be pulled to it.
Inputs
| Name | ID | Description | Type |
|---|---|---|---|
| Planes | Pl | Set of planes on surface to tween through | Plane |
| Surface | S | Surface to tween plane on | Surface |
| Factor | F | Tween factor (0.0 = Plane at Pl start, 1.0 = Plane at Pl end), unless Normalized is False | Number |
| Normalized | N | If False, the rules for factor are (0.0 = Plane at index 0, Index number of last plane = Plane at last index) The tween factor range from one plane to the next plane in the list is: Index number of a plane = the plane at that index, Index number of the next plane = the next plane in the list, factors between the plane index numbers will be the corresponding tweens. For instance: A tween factor of 2.5 will result in a tween plane halfway between the plane at index 2 and the plane at index 3. | Boolean |
| Equalized | E | If True, tween distribution is evaluated along the tween path without considering the locations of the input plane set | Boolean |
| Weighted | W | If True, tween distribution is weighted by the input plane set and the tween path curvature | Boolean |
| Loopback | L | If True, allow the tween path to continue from the end back to the start as a closed loop (if Normalized is False, increase the tween factor range maximum by 1) | Boolean |
| Degree | D | Curvature degree of the tween path, degree should be a positive odd number | Integer |
| Interpolation Type | I | Determines how the tween path is interpolated 0 = Linear 1 = Chord 2 = Square Root 3 = Uniform | Integer |
| Quaternion | Q | Interpolate with quaternion rotation | Boolean |
Outputs
| Name | ID | Description | Type |
|---|---|---|---|
| Tween | T | Resulting tween plane on surface | Plane |
Site design © Robin Rodricks.
Pufferfish and associated data © 2025 Michael Pryor.
Rhinoceros and Grasshopper are registered trademarks of Robert McNeel & Associates.
Hosted by GitHub